Physics A: Problem Set 18: Refraction

recommended reading

High Marks:	4:41–4:47, 4:53–4:55
Barron's Let's Review:	11.6 Refraction, 12.6 Refraction
physics.info:	Refraction
Wikipedia:	Refraction, Snell's law, Total internal reflection
HyperPhysics:	Refraction of light
Khan Academy:	Reflection and refraction
YouTube:	Upside down glasses challenge
Mr. Machado:	16 Refraction, 18 Refraction and Reflection in 2018 Regents Physics Exam, 19 Refraction and Reflection in 2019 Regents Physics Exam

classwork

1. A ray of light is traveling from air to crown glass. The angle that this ray makes with the surface of the glass is 30°. Determine each of the following angles…
   1. the angle of incidence
   2. the angle of reflection
   3. the angle of refraction
   4. the angle between the reflected and refracted rays
   5. the angle between the incident and refracted rays
   6. the angle between the incident and reflected rays

   Start with a sketch. Let's make the surface horizontal, because we gotta pick something. Label one side air. Label the other side crown glass. Add an incident ray 30° above the surface. Add a normal to the surface at the point where the ray strikes the surface, since angles in geometric optics are measured from the normal. Sketch a reflected ray that looks symmetric to the incident ray, since it's obeying the law of reflection. Sketch in a transmitted ray that's refracted toward the normal, since the ray is entering a medium whe the speed of light is slower.

   

   1. The angle of incidence is measured from the normal, not the surface. Use the compliment of 30°

      90° − 30° = 60°

   2. The angle of reflection equals the angle of incidence. That's the law of reflection.

      60° = 60°

   3. Use Snell's law to compute the angle of refraction.

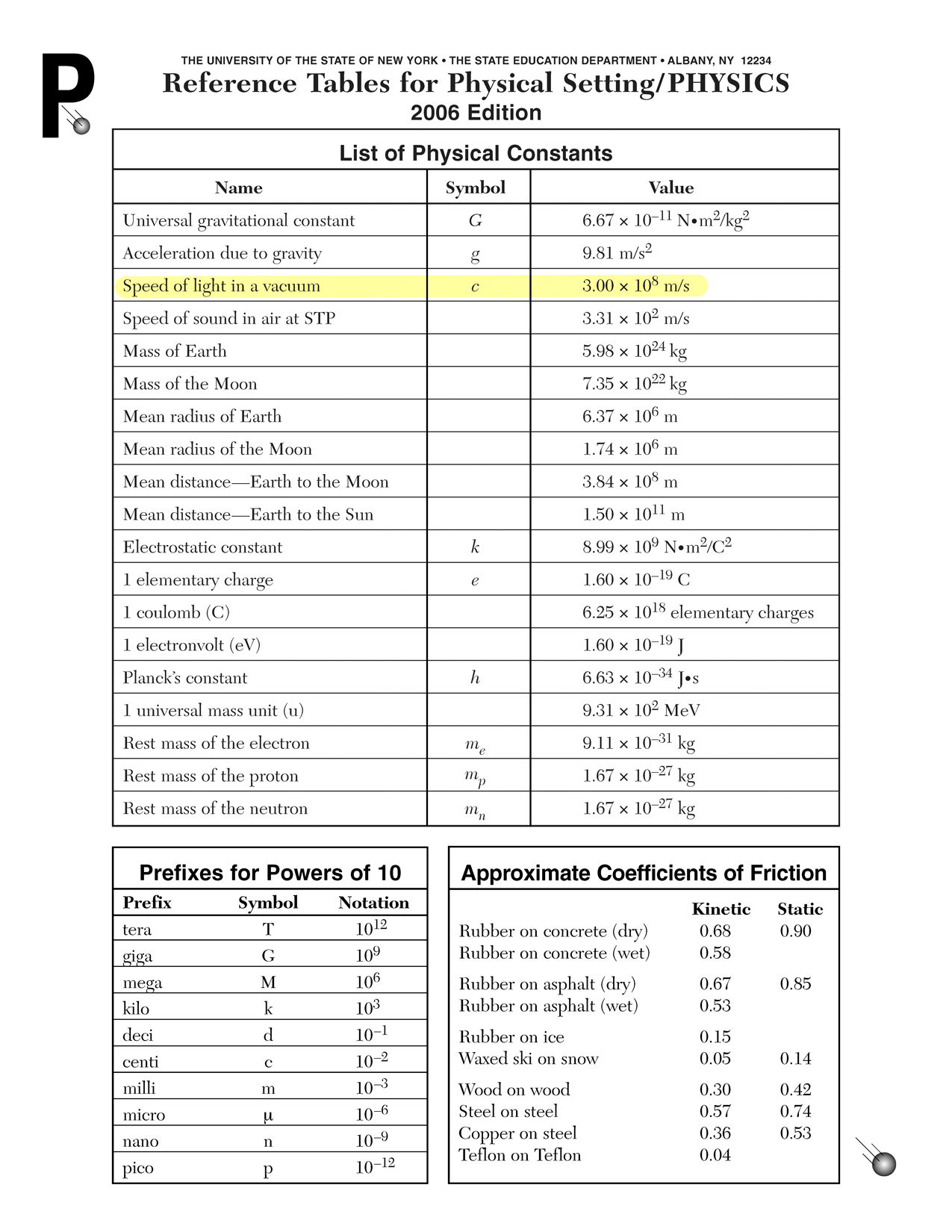
      n1 sin θ1 =	n2 sin θ2
      (1.00)(sin 60°) =	1.52 sin θ2
      θ2 =	35°

   4. Subtract the two angles on the right side of the normal from 180° to determine the angle between the reflected and refracted rays.

      180° − 60° − 35° = 85°

   5. Add the two angles adjacent to the right angle in the lower left corner to determine the angle between the incident and refracted rays.

      30° + 90° + 35° = 155°

   6. Double the angle of incidence to determine the angle between the incident and reflected rays.

      60° + 60° = 120°

   

2. The diagram below shows a ray of light (A) incident upon an air-water interface. Several possible rays (B–K) are also shown.

   

   1. Using the protractor in the diagram, measure the angle of incidence.
   2. Using the law of reflection, determine the angle of reflection, then select the lettered ray that best represents the reflected ray.
   3. Using Snell's law, determine the angle of refraction, then select the lettered ray that best represents the transmitted ray.

   1. The angle of incidence is the angle between a line normal to the interface and the incident ray. Using the protractor supplied we get 63°. You can get this number by just counting off the tick marks, or by doing a little math. The incident ray is at 153° and the normal to the interface is at 90°.

      153° − 90° = 63°

   2. According to the law of reflection, the angle of reflection equals the angle of incidence. So once again the answer is 63°. Ray D best represents this direction.

   3. Snell's law is usually written like this.

      n₁ sin θ₁ = n₂ sin θ₂

      For this problem…

      n1 =	1.00 (air)
      θ1 =	63°

      n2 =	1.33 (water)
      θ2 =	?

      Substituting these numbers…

      (1.00)(sin 63°) = 1.33 sin θ₂

      gives us this answer…

      θ₂ = 42°

      Ray G best represents this direction.

   

homework

3. Using the Reference Tables for Physical Setting/PHYSICS, identify a likely material if the speed of light (v) in the material is the following fraction of the speed of light (c) in a vacuum…
   1. v = ⅔c
   2. v = ¾c
   3. v = ⅗c

   Use the index of refraction equation.

   n =	c
   	v

   Replace the denominator with a fraction of the speed of light. The speed of light cancels out and the original fraction inverts. Compute this fraction as a decimal. Pick the substance with the closest index of refraction. Do it three times.

   1. This is probably lucite.

      n =	c	=	3	= 1.50
      	⅔c		2

   2. This is probably water.

      n =	c	=	4	= 1.33
      	¾c		3

   3. This is probably flint glass.

      n =	c	=	5	= 1.66
      	⅗c		3

4. The diagram below shows an interface between an unspecified transparent liquid and a piece of Lucite. An incident ray of light that has been partially reflected and partially transmitted at the interface is also shown.

   

   1. Determine the angle of incidence.
   2. Determine the angle of reflection.
   3. Determine the angle of refraction.
   4. Determine the index of refraction of the unspecified liquid.
   5. What is the unspecified liquid?

   1. Using the protractor supplied, the angle between the incident ray and the normal is 44°.

   2. Using the protractor supplied, the angle between the reflected ray and the normal is 44°. This agrees with the law of reflection, which states that the angle of incidence equals the angle of reflection.

   3. Using the protractor one last time, the angle between the transmitted ray and the normal is 39°.

   4. This part has to be done using Snell's law…

      n₁ sin θ₁ = n₂ sin θ₂

      where…

      n1 =	? (unspecified)
      θ1 =	44°

      n2 =	1.50 (Lucite)
      θ2 =	39°

      Substituting these numbers…

      n₁ sin 44° = (1.50)(sin 39°)

      gives us this answer…

      n₁ = 1.36

   5. The unspecified liquid is most likely ethyl alcohol or acetone. Other liquids are also certainly possible. These two show up commonly in reference sources as having an index of 1.36.