The Physics
Hypertextbook
Opus in profectus

Music and Noise

search icon

Problems

practice

  1. According to Galileo…

    Especially harsh is the dissonance between notes whose frequencies are incommensurable; such a case occurs when one has two strings in unison and sounds one of them open, together with a part of the other which bears the same ratio as the side of a square bears to the diagonal….

    Galileo Galilei, 1638

    Identify this interval on the equal tempered scale.
  2. Determine the beat frequency between C4 and G4 (a perfect fifth) when played on an equal tempered scale where A4 = 440 Hz.
  3. Verify the following statements about these Fourier series made on Wikipedia.
    1. A sawtooth wave "contains odd and even harmonics that fall off at −6 dB/octave."

      y = sin x − 12 sin 2x + 13 sin 3x − 14 sin 4x +…

      y = ∑(− 1)n +1 sin nx
      n
    2. A square wave "contains odd harmonics that fall off at −6 dB/octave."

      y = sin x + 13 sin 3x + 15 sin 5x + 17 sin 7x +…

      y = ∑1 sin(2n − 1)x
      2n − 1
    3. A triangle wave "contains odd harmonics that fall off at −12 dB/octave."

      y = cos x + 19 cos 3x + 125 cos 5x + 149 cos 7x +…

      y = ∑1 cos(2n − 1)x
      (2n − 1)2
  4. Write something completely different.

numerical

  1. The often quoted ideal range of human hearing is 20 Hz to 20 kHz. How many octaves is this?
  2. Determine the frequencies of the 13 labeled notes on the fragment of a keyboard shown below for an equal tempered scaled based on A = 435 Hz (International Pitch of 1891).
    C♯ D♯ F♯ G♯ A♯
    C D E F G A
    435
    Hz    		 B C
  3. Read the following passage on pigeons (Columba livia)…

    Pigeons have extraordinarily sensitive vision and hearing, scientists say, They can see beyond the spectrum of light visible to humans, into the ultraviolet range. They can hear in extremely low frequencies far beneath what humans can detect, down to something like 13 octaves below middle C on the piano. That ability is probably critical to a bird that is meant to migrate long distances and is at the mercy of weather patterns.

    New York Times, 1991

    According to the information this reporter found, how low can a pigeon hear?

  4. The lowest note in the universe has been playing for the last 2.5 billion years. The instrument is a black hole 250 million light years away from Earth in the center of Perseus cluster of galaxies. We think of space as being empty and it almost is, but in actuality space is filled everywhere with a gas or plasma that ranges in density from thin (one atom per cubic centimeter in the space between the planets) to very, very, very, very, very, very thin (one atom per cubic meter in the space between galaxies). The black hole at the center of the Perseus cluster is consuming matter and belching out energy in a manner that has imprinted a pattern on the intergalactic medium that looks just like a sound wave. (See the images below.)

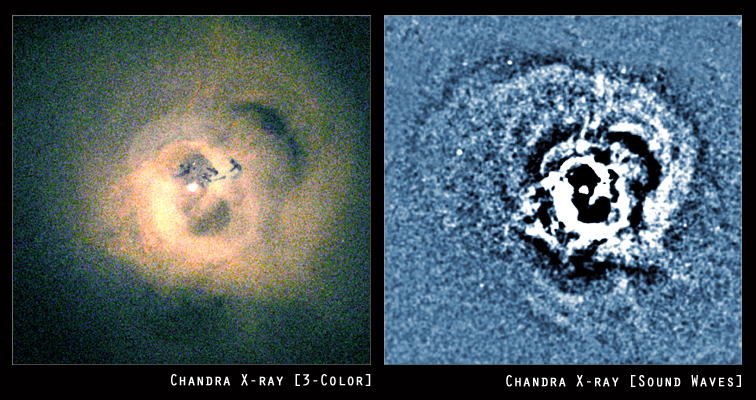    Side by side x-ray images of the Perseus cluster processed in differnt waysSource: NASA/CXC/IoA/Fabian

    In the words of the discoverers.

    If the ripples are pressure (sound) waves moving at constant speed (about 1,170 km s−1 for a temperature of 5 keV) then their separation (wavelength) of about 11 kpc means a period of about 9.6 × 106 yr.

    Andrew Fabian, et al., 2003

    Apply a bit of physics to these numbers and you will find a bit of a problem. The most reliable measurement has got to be the wavelength. This is a measurement determined by the geometry of the image. Everything else has to be calculated or inferred.

    1. Use the wavelength and period quoted above to calculate the wave speed. How does your answer compare to the reported wave speed?
    2. Use the wavelength and wave speed quoted above to determine the period. How does your answer compare to the reported period?
    3. What's going on with these numbers? (I don't know the answer to this question, by the way.)

    With such an incredibly long period, this sound wave has to be "the lowest note in the universe". Somewhere in the report of this discovery to the mass media, that's how it was phrased. Since I live in New York City, let's assume that the New York Times was the first to report this to the general public.

    Astronomers say they have heard the sound of a black hole singing. And what it is singing, and perhaps has been singing for more than two billion years, they say, is B flat — a B flat 57 octaves lower than middle C.

    New York Times, 2003

    Assigning particular frequencies to notes is not that easy to do. Music isn't about frequencies, it's really about intervals. Notes are defined in terms of the ratios they make with some standard frequency, not by what frequency they have. You change that standard frequency and you change the note. Does the black hole in the Perseus cluster emit a note equivalent to an extremely low B♭ or is it closer to an extremely low A or B? Divide the frequency of the sound waves emitted by the black hole by 57 octaves (257) and see where it lands on each of the following scales. What "note" is the black hole at the center of this galaxy emitting if we use…

    1. the American Standards Association (ASA) of 1936
    2. the International Pitch value of 1891
    3. Hermann von Helmholtz's "Scientific" or "Philosopher's" scale
    Apply three musical scales to this event
    standard year A4 B♭4 B4
    d. American Standards Association 1936 440.00 Hz 466.16 Hz 493.88 Hz
    e. International pitch 1891 435.00 Hz 460.87 Hz 488.27 Hz
    f. Helmholtz's scale 426.67 Hz somewhere in between 480.00 Hz

statistical

  1. Complete the following table for the twelve intervals of the just intonation scale…
    interval consonance
    name ratio per cent rank
    unison 1:1 100% 1
    minor second 16:15
    major second 9:8 11%
    minor third 6:5
    major third 5:4 20%
    perfect fourth 4:3 25% 4
    tritone 7:5
    perfect fifth 3:2 33% 3
    minor sixth 8:5
    major sixth 5:3 20%
    minor seventh 16:90
    major seventh 15:80 7%
    octave 2:1 50% 2