Interference and Superposition
Practice
practice problem 1
Write something.
solution
Answer it.
practice problem 2
Write something else.
solution
Answer it.
practice problem 3
Graph the following Fourier series with enough detail that you can determine basic shape of each wave.
y = sin x + 13 sin 3x + 15 sin 5x + 17 sin 7x +…
y = ∑ 1 sin(2n − 1)x 2n − 1 y = sin x − 12 sin 2x + 13 sin 3x − 14 sin 4x +…
y = ∑ (− 1)n +1 sin nx n y = cos x + 19 cos 3x + 125 cos 5x + 149 cos 7x +…
y = ∑ 1 cos(2n − 1)x (2n − 1)2
solution
I summed the first ten terms for all three functions, but you don't need to take the series out that far to get an idea of its basic shape. Each resulting "wave" is named for its shape.
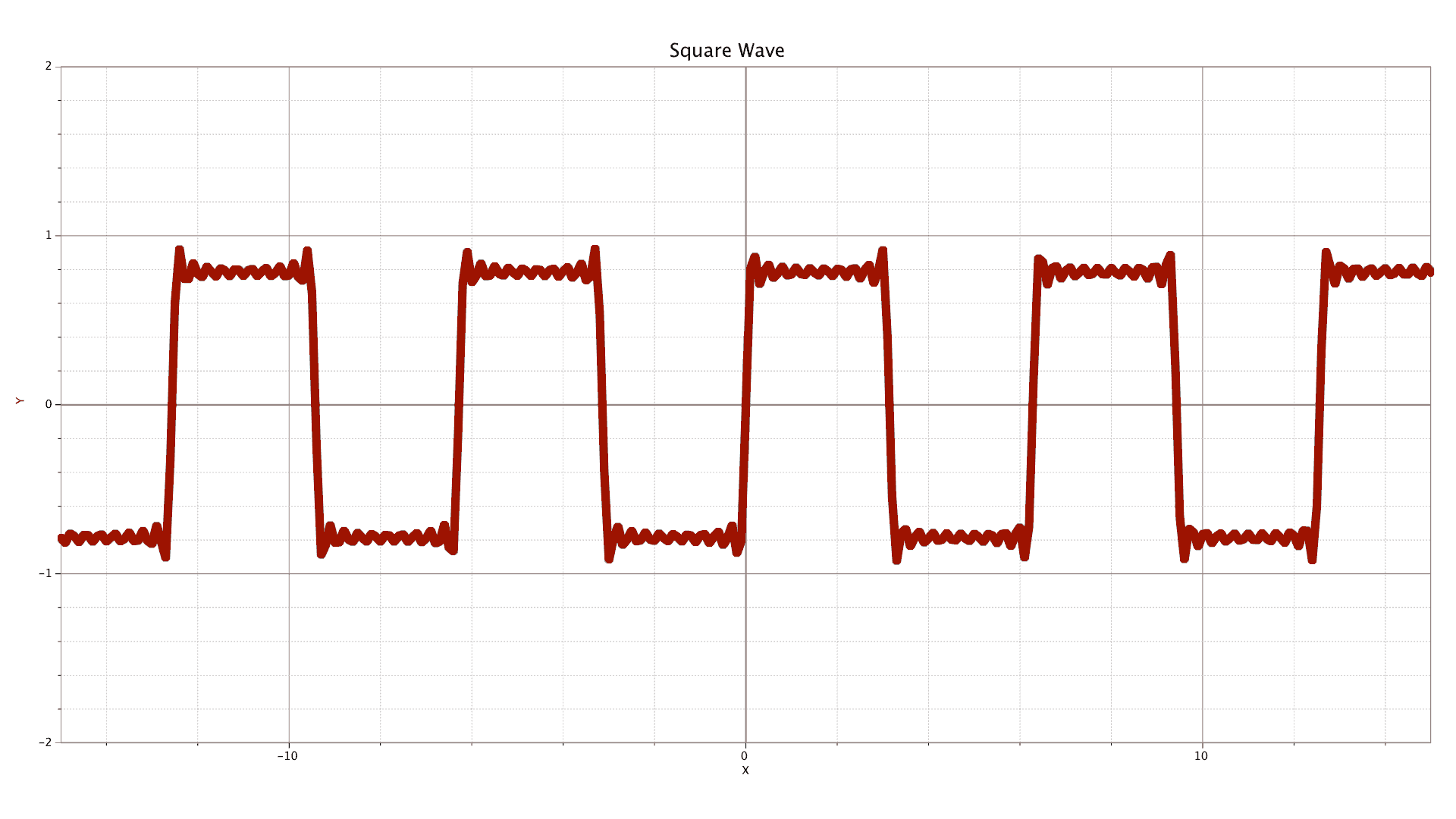
Here we have a square wave (although this one is more rectangular than square).
y = sin x + 13 sin 3x + 15 sin 5x + 17 sin 7x +…
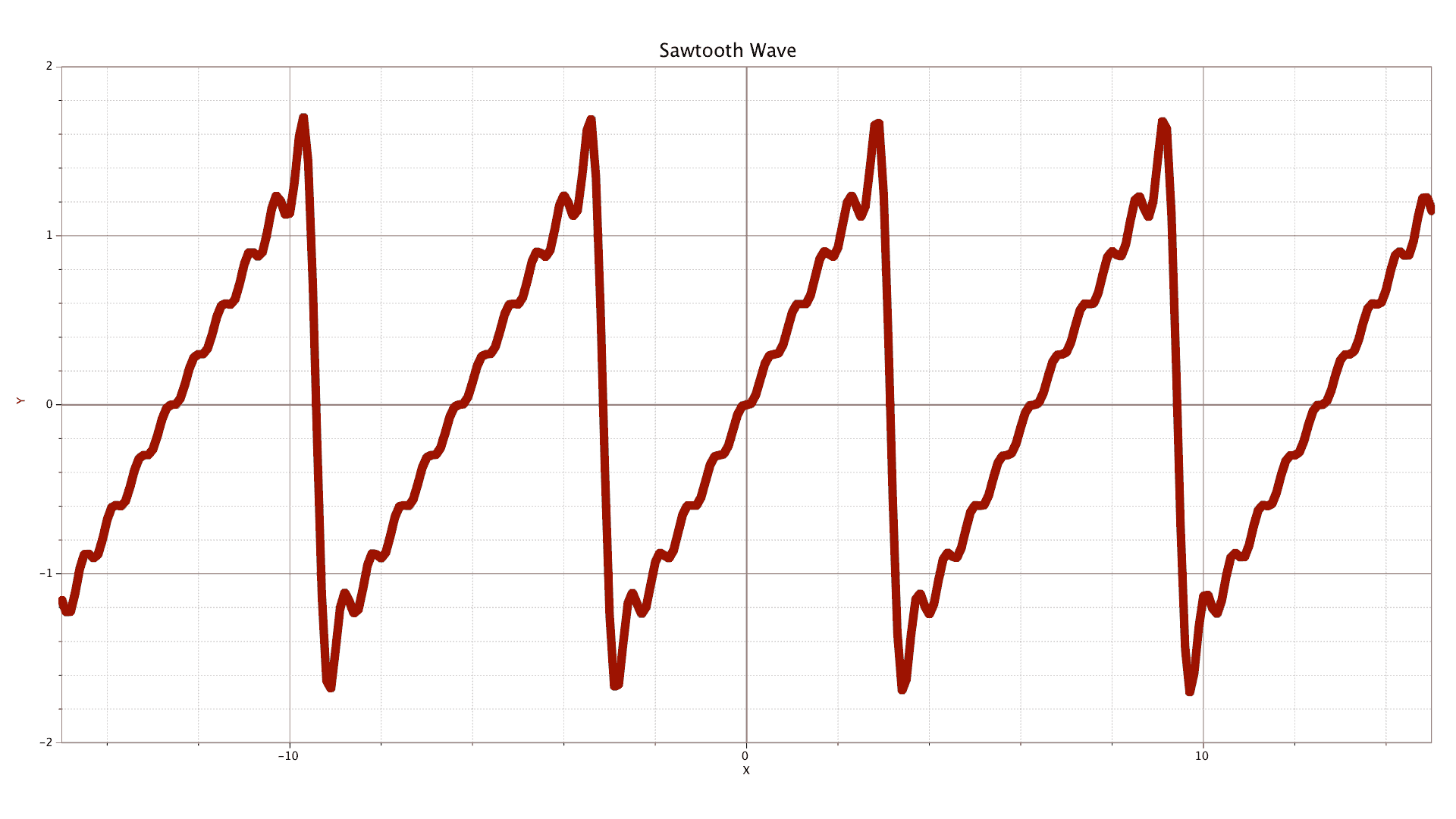
This is a sawtooth wave, also known as a ramp wave.
y = sin x − 12 sin 2x + 13 sin 3x − 14 sin 4x +…
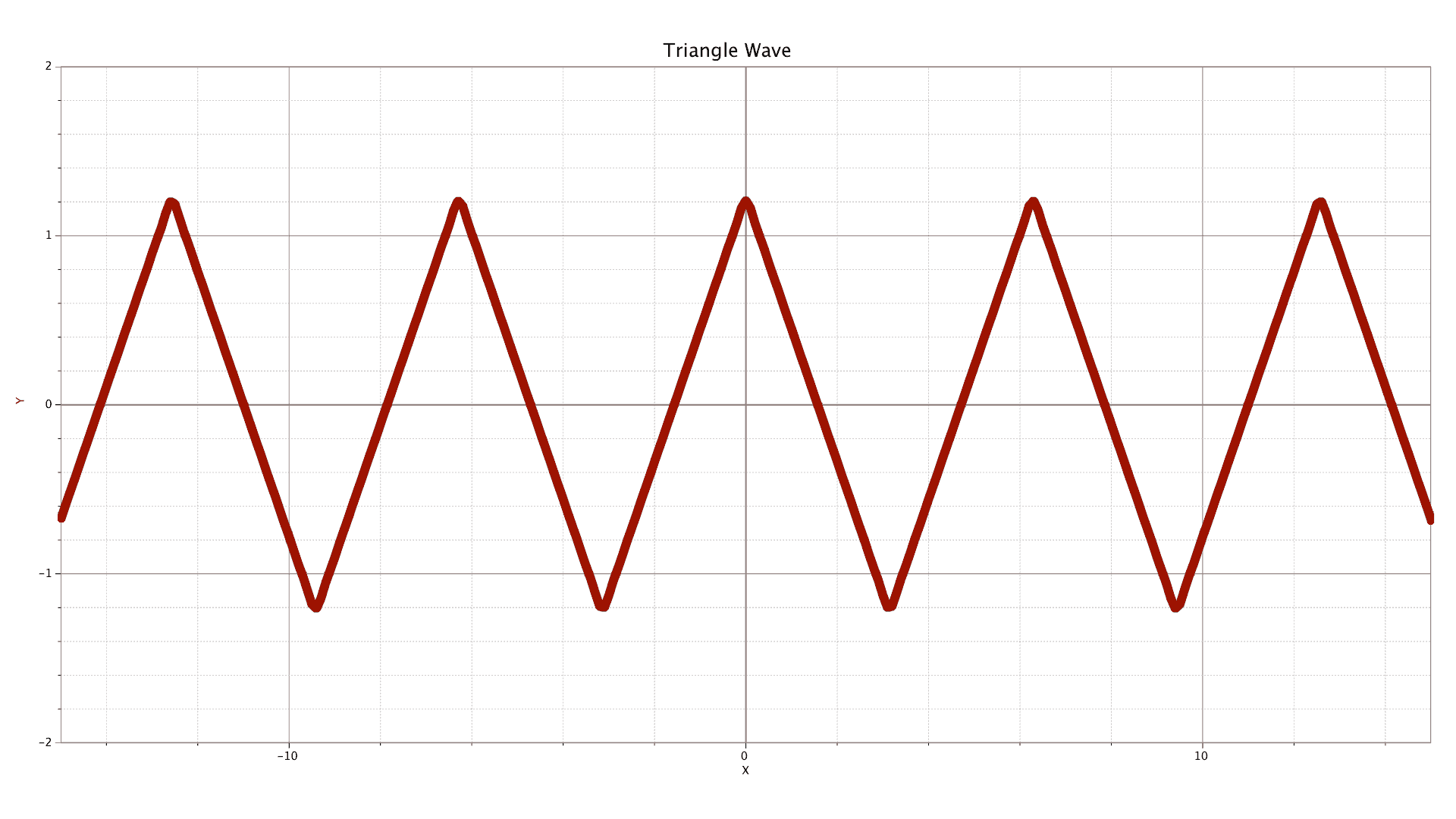
And we end with a triangle wave. This one converges to its final shape more quickly.
y = cos x + 19 cos 3x + 125 cos 5x + 149 cos 7x +…
practice problem 4
Write something completely different.
solution
Answer it.