Curve Fitting
Practice
practice problem 1
- A six pack of tablet computers cost $250. What would two dozen of these devices cost?
- Four landscapers can lay 8 meters of brick sidewalk in 6 hours. How long would it take one landscaper to do the job alone?
- The floor of a 3 meter by 3 meter private office is covered by 100 tiles. How many tiles are needed for a 12 meter by 12 meter shared office?
- The density of water is 1,000 kilograms per cubic meter. What is the density of a cup of water?
- A student takes 10 minutes to walk from home to school at her normal pace. If she runs twice as fast as she normally walks, how long does it take her to run from home to school?
- Twelfth grade students consume twice as much food during lunch as do first graders. A class of 12 first graders consume 6,000 calories. How many calories does a class of 24 twelfth graders consume?
- Two students watch an instructional video together. The video lasts 12 minutes. How long does the video last if three students watch it?
- A pump at a filling station delivers 12 liters of gasoline for $18. How much gas can be bought from this same pump with $6?
- A single prep cook needs 1 hour to peel 120 carrots. How many prep cooks would it take to peel 240 carrots in 20 minutes?
- A physics student gets a grade of 80% on the first quiz of the semester and 85% on the second quiz. What grade does the student get on the third quiz?
solution
A six pack of tablet computers cost $250. What would two dozen of these devices cost?
Answer: $1000
This problem is an example of a direct relationship. As the number of tablets purchased increases so does the number of dollars spent. Two dozen is four times more than six. Four times more tablets means four times more money.
24 tablets = 4× more 6 tablets 4 × $250 = $1,000
Here's another approach. When two quantities are directly proportional, their ratio is constant.
a ∝ b ⇔ a = k b In this case, that ratio is the unit price.
price = constant
(unit price)tablet $250 = x 6 tablets 24 tablets x = $1000
Four landscapers can lay 8 meters of brick sidewalk in 6 hours. How long would it take one landscaper to do the job alone?
Answer: 24 hours
This problem is an example of an inverse relationship. As the number of people working on a job decreases, the time it takes to finish the job increases. One person is one fourth of four people. One fourth the workers means four times more work for that one person.
1 person = ¼ as many 4 people 4 × 6 hours = 24 hours
Here's another way to think about this. When two quantities are inversely proportional, their product is constant.
a ∝ 1 b ⇔ ab = k In this case, the constant is the number of person hours.
number of
workers× hours spent
working= constant
(person hours)(4 people)(8 hours) = (1 person)x
x = 24 hours
The floor of a 3 meter by 3 meter, private office is covered by 100 tiles. How many tiles are needed for a 12 meter by 12 meter, shared office?
Answer: 1,600 tiles
This is a problem where one quantity is proportional to the square of the other. The linear dimensions of the floor are both quadrupling — four times longer and four times wider or sixteen times more area.
(12 m)2 = 42× more = 16× more (3 m)2 16 × 100 tiles = 1,600 tiles
The density of water is 1,000 kg per cubic meter. What is the density of a cup of water?
Answer: 1,000 kg/m3
The density of water is an intensive property, which means it doesn't matter how much of it you have. Having more or less water does not make it more or less dense.
Mathematically, density is independent of volume or, to say it another way, volume is not a factor that affects the density of water. This is not quite the same thing as saying it's constant. The density of water is affected by temperature, phase, and salinity, so it doesn't have a constant value. Pedantic readers would insist that the problem specify the temperature, phase, and salinity — something like "pure liquid water at 4 °C". The unstated rule of an introductory textbook like this one is…
Don't overthink problems.
A student takes 10 minutes to walk from home to school at her normal pace. If she runs twice as fast as she normally walks, how long does it take her to run from home to school?
Answer: 5 minutes
Most people know intuitively that twice as fast means half the time. This is an example of an inverse relationship. Time is inversely proportional to speed in formal language.
t ∝ 1 v The symbol t for time is obvious. The symbol v for speed comes from the closely related word velocity. This comes from the definition of speed as the rate of change of distance with time.
v = ∆s ∆t The symbol s is used for distance because s is the first letter in the Latin word for distance, spatium. The Greek letter ∆ (delta) is used to indicate that the change in the quantity is what matters.
Time is the denominator of a fraction on the right side of the equals sign. Speed is the numerator of a fraction on the left side (a fraction where the denominator is implied to be one). Numerator on one side. Denominator on the other. That makes those two quantities inversely proportional.
Twelfth grade students consume twice as much food during lunch as do first graders. A class of 12 first graders consume 6,000 calories. How many calories does a class of 24 twelfth graders consume?
Answer: 24,000 calories
There are twice as many twelfth graders and they eat twice as much. Double 6,000 calories and double it again.
2 × 2 × 6,000 calories = 24,000 calories
Mathematically, we have something like this…
calories
consumed= calories
per student× number of
studentsWhich is essentially this…
dependent
variable= rate × independent
variableWhich we could shorthand to…
y = kx
In this problem, both the rate (calories per student) and the independent variable (number of students) are doubling. This makes the independent variable (calories consumed) quadruple.
4y = 2k2x
Two students watch an instructional video together. The video lasts 12 minutes. How long does the video last if three students watch it?
Answer: 12 minutes
Don't overthink problems.
A pump at a filling station delivers 12 liters of gasoline for $18. How much gas can be bought from this same pump with $6?
Answer: 4 liters
Filling stations sell gasoline like gold — as a commodity. There are no things like connection fees or bracket pricing. The rate is set at the pump and does not vary with amount purchased, customer loyalty, or model of car. One way to solve this problem is by computing the rate (the unit price) set for this pump.
price = constant
(unit price)volume $18 = $1.50/L 12 L Divide the amount of money available by the rate to get the volume dispensed.
$6 = 4 L $1.50/L Another way to think about this is that $6 is one third of $18.
$6 = ⅓ as much $18 Gas is directly proportional to cash.
gas ∝ cash
One third less money means one third less gas.
⅓ × 12 liters = 4 liters
A single prep cook needs 1 hour to peel 120 carrots. How many prep cooks would it take to peel 240 carrots in 20 minutes?
Answer: 6 prep cooks
More workers are needed to get a job done in less time. The number of workers is inversely proportional to the time required to do an amount of work.
workers ∝ 1 time More workers are needed to get more work done. The number of workers is directly proportional to the amount of work to be done.
workers ∝ work
Twice as much work…
240 carrots = 2× more work 120 carrots in one third the time…
1 hour = ⅓ as much time 20 minutes means six times more workers are needed…
2 × 3 × 1 prep cook = 6 prep cooks
A physics student gets a grade of 80% on the first quiz of the semester and 85% on the second quiz. What grade does the student get on the third quiz?
Answer: This question has no answer.
practice problem 2
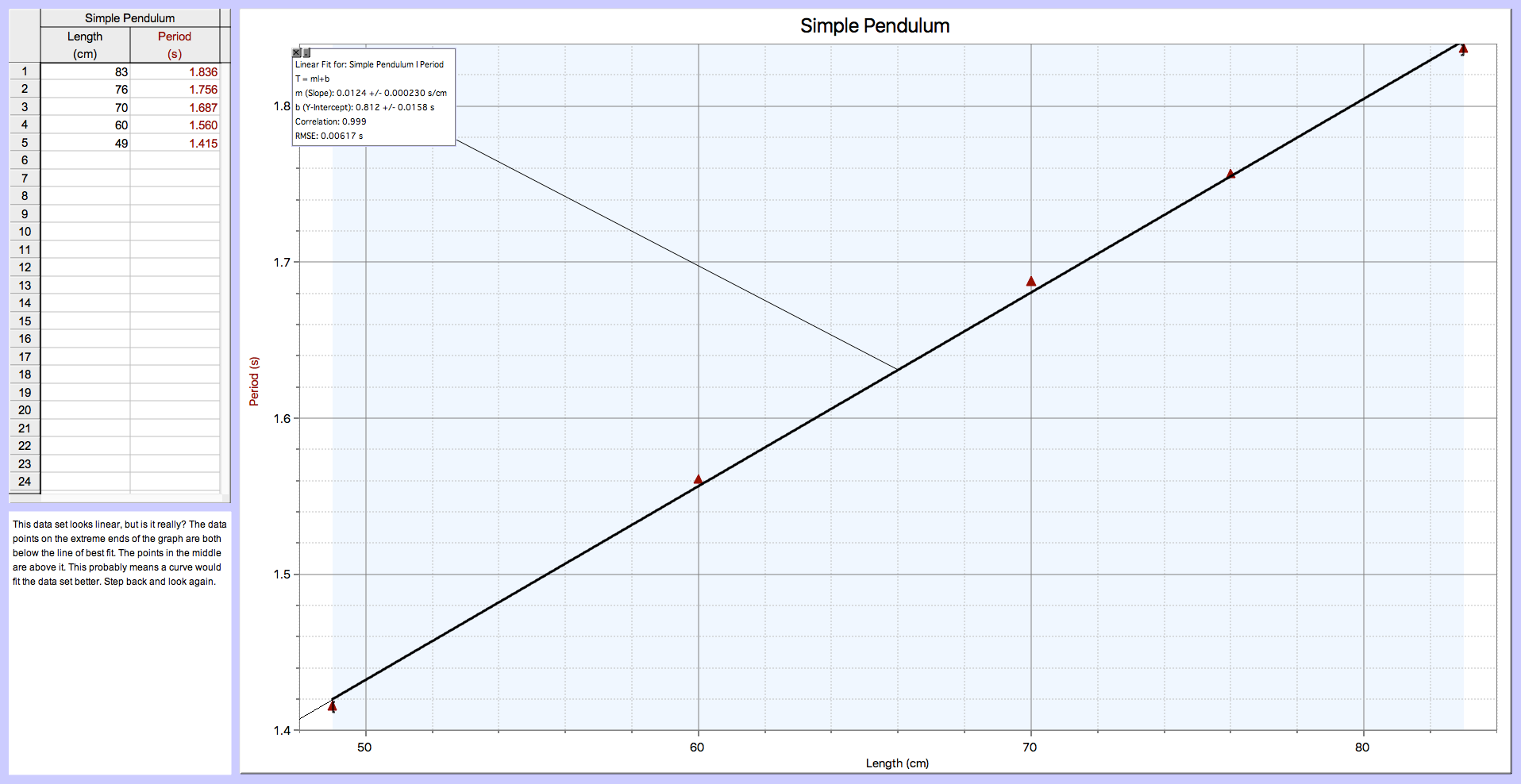
In this experiment, simple pendulums of different lengths were constructed and their periods measured. This data set looks linear, but is it really? What effect does length have on the period of a simple pendulum?
solution
This data set looks linear, but is it really? The data points on the extreme ends of the graph are both below the line of best fit. The points in the middle are above it. This probably means a curve would fit the data set better. Step back and look again.
The relationship is not linear. A power curve fit shows that the period of a simple pendulum is proportional to the square root of its length. The best fit power is approximately ½ (0.495). The shape of the curve is a horizontal parabola (just the top half of it).
A variable power fit where the power was set to ½ does not fit as well as the best fit power of 0.495, but it is more appropriate. Relationships between simple quantities (like period and length) tend to be simple (like how ½ is simpler than 0.495). The period of a simple pendulum is proportional to the square root of its length.
practice problem 3
Snow rarely gets a chance to melt in Antarctica, even in the summer when the sun never sets. In the interior of the continent, the temperature of the air hasn't been above the freezing point of water in any significant way for the last 900,000 years. The snow that falls there accumulates and accumulates and accumulates until it compresses into rock solid ice — up to 4.5 km thick in some regions. Since the snow that falls is originally fluffy with air, the ice that eventually forms still holds remnants of this air — very, very old air. By examining the isotopic composition of the gases in carefully extracted ice cores we can learn things about the climate of the past. By extension we might also be able to predict some things about the climate of the future.
Columns
- Age of air (years before present)
- Temperature anomaly with respect to the mean recent time value (°C)
- Carbon dioxide concentration (ppm)
- Dust concentration (ppm)
Adapted from Petit et al. 1999
Questions…
- CO2
- Construct a set of overlapping time series graphs for CO2concentration and temperature anomaly.
- Construct a scatter plot of temperature anomaly vs. CO2concentration.
- How are atmospheric carbon dioxide concentration and temperature anomaly related?
- What temperature anomaly might one expect given current atmospheric CO2levels?
- Dust
- Construct a set of overlapping time series graphs for dust and temperature anomaly.
- Construct a scatter plot of temperature anomaly vs. dust concentration.
- How are atmospheric dust concentration and temperature anomaly related?
- What global average temperature anomaly might one expect from exceptionally high levels of atmospheric dust?
solution
-
CO2
Here are the overlapping time series graphs. The data show a definite correlation. The two quantities go up and down in near synchrony.
Here's the scatter plot of the two time-varying quantities plotted against one another. The data forms a dense cloud that is roughly oval shaped. The best fit line slices nicely through the data.
Temperature varies linearly with atmospheric carbon dioxide concentration. Low CO2levels go with a cooler climate and high CO2levels go with a warmer climate.
What does our linear regression analysis predict given current carbon dioxide levels of about 400 ppm?
y = mx + b
y = (0.0908 °C/ppm)(400 ppm)− 25.23 °C
y = +11 °CThe current consensus among working climate scientists is that the globe will warm +5 °C on average over the course of the 21st century. The increase is expected to be smaller than average near the equator and greater than average near the poles. Since the Vostok ice cores were collected in Antarctica, our prediction of approximately +10 °C is right in line with those made by more sophisticated means.
Correlation is not causation, however. Graphs like those used in this problem cannot tell us whether carbon dioxide affects temperature, temperature affects carbon dioxide, or some third factor is affecting both. We need a theoretical model that describes which way the cause and effect work. That model is described in more detail in the section of this book that deals with heat transfer by radiation.
Carbon dioxide is a greenhouse gas. Its role in atmospheric thermodynamics is much like the glass in a greenhouse. It is transparent to visible light, but not to infrared. Visible light easily punches through the atmosphere. It is absorbed by the ground and then reradiated as infrared. The infrared is partly blocked by the atmosphere and has a hard time escaping out into space. This little delay keeps the Earth comfortably warm. Water vapor, carbon dioxide, methane, and other gases have been shown to play a significant role in this process. They all interact with infrared radiation. These properties have been measured in tabletop laboratory experiments that had no direct connection to climatology.
Atmospheric carbon dioxide levels have increased steadily over the past 100 to 150 years. This is due to the burning of coal, petroleum, and natural gas as well as deforestation and other changes in land use associated with the Industrial Revolution. During this same time period, average global temperatures have been generally increasing and there is no reason to believe that this trend will quit anytime soon. Climate models all show that as long as CO2concentrations stay somewhere around their turn of the 21st century levels, global temperatures will continue to increase for the next 100 years. This conclusion is based on solid scientific reasoning and is regarded by nearly all climate scientists as valid. The scientific questions that remain unanswered are: how can we increase the precision and reliability of our global climate predictions and what effect will the inevitable changes have on life as we know it? The question of what is to be done about this is is a political, not scientific, question.
-
Dust
Here are the overlapping time series graphs. The correlation with temperature is not as evident for dust as it was for CO2 since the changes are in the opposite direction. High levels of dust seem to correlate with low temperatures.
The relation between dust and temperature becomes more evident when graphed as a scatter plot. It appears that temperature decreases with increasing dust, but this decrease levels off after a while. The relationship appears to have a horizontal asymptote like an exponential approach function.
Atmospheric dust correlates to a negative temperature anomaly that exponentially approaches a minimum value.
As dust concentration increases, the exponential term of our curve fitting function approaches zero leaving the constant term to stand by itself. This is the limit or asymptote of our curve fit.
y = ae−bx − c ymin = − c = −7.6 °C So what is going on here? Does dust cause temperatures to drop or do low temperatures make the dust fly? The answer to this question is not so simple. Here we have a real problem of determining causation.
Water vapor, carbon dioxide, methane, and the other greenhouse gases absorb and reradiate infrared radiation because the natural vibrational frequencies of these molecules lie in the infrared part of the electromagnetic spectrum. They don't vibrate at visible light frequencies, which is why they are all transparent to the light that we see with our eyes.
Dust particles are large compared to molecules. They are also larger than a wavelength of infrared or visible light. Because of this, they are essentially obstacles to infrared and visible light waves. When the sky is full of dust, light has a hard time making it down to the ground. The dust particles scatter a great deal of solar energy back into space and the Earth is a little bit cooler as a result. Large volcanoes can spread so much dust into the atmosphere that they sometimes have a measurable effect on climate. The 1991 eruption of Mount Pinatubo in the Philippines caused a globally averaged temperature anomaly of −0.3 °C that lasted two years.
Well actually, that last statement isn't quite right. Mount Pinatubo did spread a lot of ash around the globe (resulting in fantastic sunsets), but the primary mechanism by which it cooled the Earth was through the injection of sulfur dioxide into the stratosphere. When SO2gets together with H2O the result is an aerosol of H2SO4— sulfuric acid. Aerosols have a greater cooling effect on climate than dust. (They are also notoriously hard to describe in climate models.)
Now let's examine the reverse causation. A cool climate is a dry one. When temperatures are low, water has a hard time evaporating. Less water vapor means less rain. Less rain means more dust. Maybe dust levels are high when the climate is cool is because a cool climate leads to more dust. If that's the case, then the last part of this problem may not be a question that can be answered with this data set.
If dust causes cooling, then the coldest dust could ever make the Earth would be around −8 °C lower than it is now. If cooling causes dust, then all we can say is that there has never been a temperature anomaly lower than −8 °C in the last 400,000 years and every time the Earth has gotten this cold it's been very dusty.
practice problem 4
An internet search engine was queried for pizzerias in the area centered on Brooklyn College. The name, phone number, and address were recorded for the first six hits. How is the building number of a pizzeria in Brooklyn affected by the last four digits of its phone number?