Conduction
Practice
practice problem 1

solution
Copper is one of the best conductors of heat available (only silver has a higher thermal conductivity), while stainless steel is a relatively mediocre conductor (mercury is one of the few metals with a lower thermal conductivity). Using copper in the base would increase the rate at which heat was transferred from the flames or heating element to the food, while using stainless steel on the sides would reduce the rate at which heat was lost from the food to the environment. Such an arrangement results in an effective cook pot that responds rapidly to changes in burner output. Capping the copper base with stainless steel seems to work against this efficiency, however.
For many applications a base that was made only of copper would probably be too effective at transferring heat. Heat applied to a small region would be transferred so rapidly that it wouldn't have time to diffuse across the pot's bottom. This would result in uneven cooking and possibly even local areas of scorching. Capping the base with stainless steel slows the immediate rate of heat transfer from the burner or heating element, but once this heat enters the copper core its high conductivity would spread the heat rapidly and evenly to all parts of the base.
There are also some esthetic issues behind this design. Copper is notoriously hard to clean, while stainless steel is, well, stainless. Cooks who insisted that their cookware sparkle at all times (even on the surfaces that are never in contact with food) would probably appreciate the use of low maintenance materials for most of the exterior. The thin, exposed band of copper near the bottom is no doubt there to catch the eye of the wandering customer.
practice problem 2
solution
Answer it.
practice problem 3
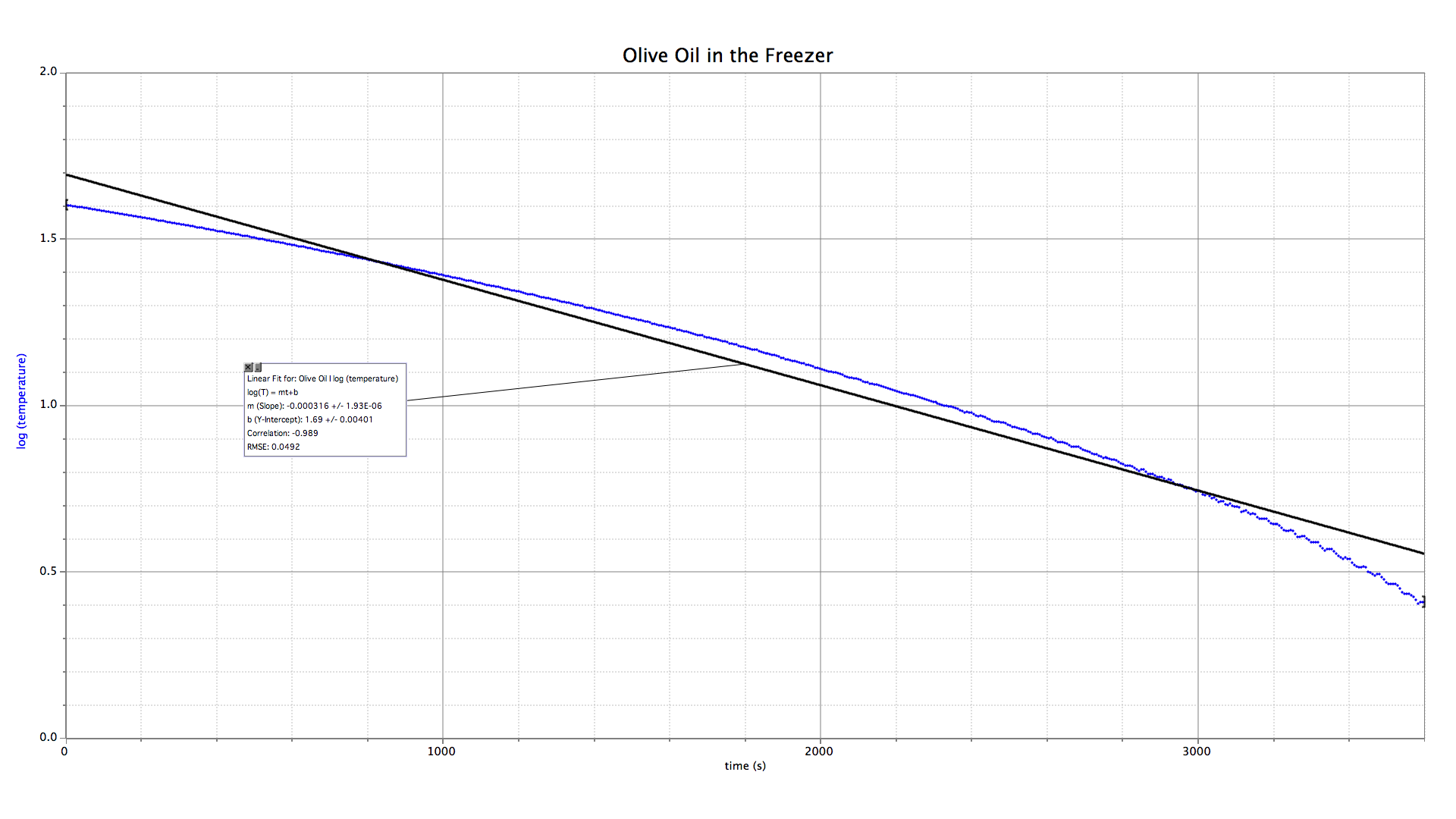
A liter of warm olive oil was placed in a freezer and allowed to solidify. Temperature measurements were taken every six seconds for one hour. Determine its final equilibrium temperature.
solution
The temperature data appear to follow an exponential decay function. An automatic curve fit returns a limit value of −11.2 °C. The fit looks good early on, but near the end of the data collection period there is a noticeable deviation, which leads me to believe that the extrapolation to the equilibrium value is unreliable.
Taking the logarithm of a quantity that varies exponentially will transform it into a linear relationship. This graph of log(temperature) vs. time does not fit a straight line, however, and is not technically exponential. The data needs to be massaged a bit to get it to fit.
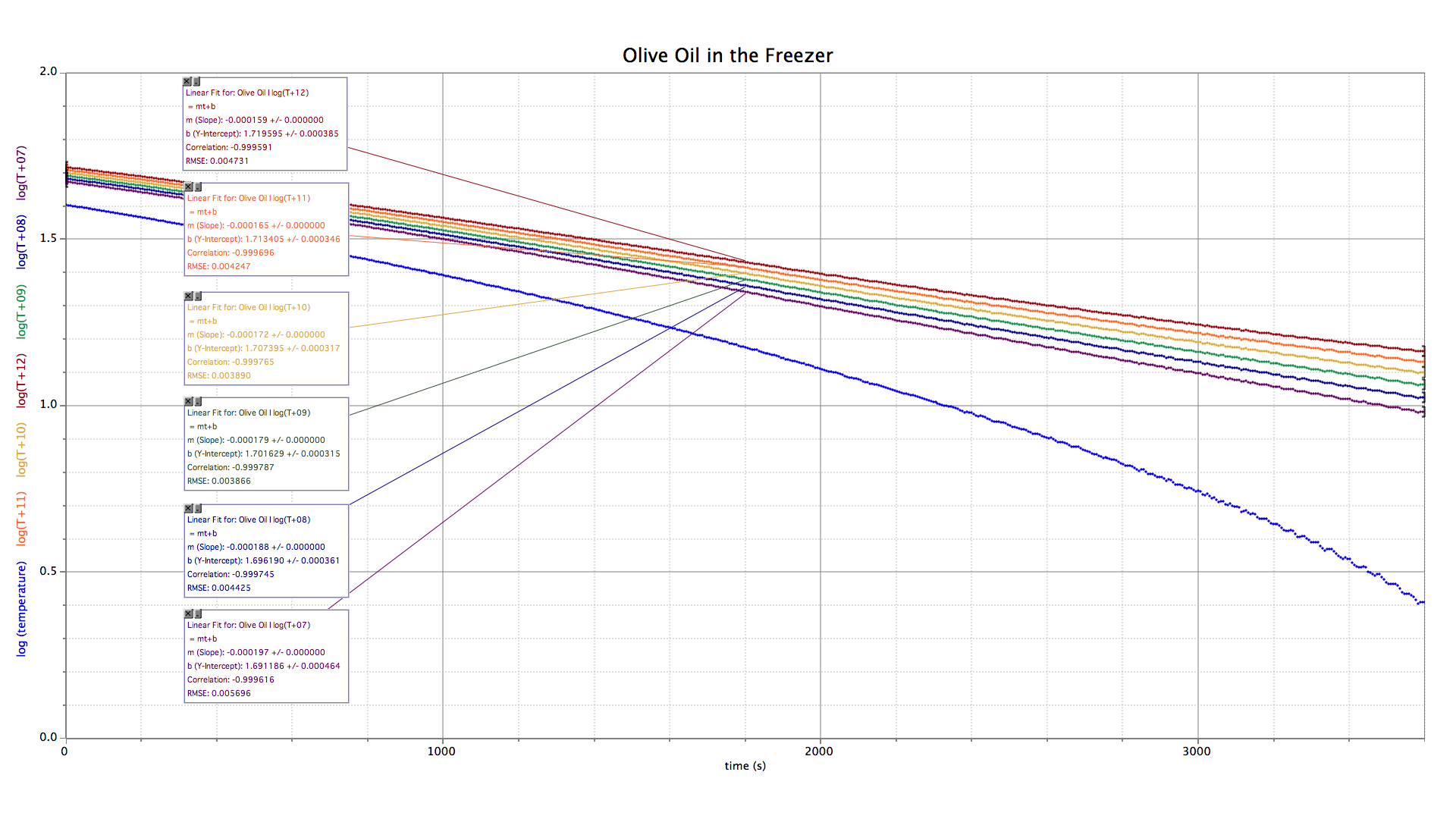
Recall that the limit of an exponential decay process is zero. But the olive oil in our freezer will obviously end up below the freezing point of water (that is, below zero celsius). In order to get our temperature data to approach zero we will add a constant number to every value. The constant that results in the best linear fit will give the final temperature of the oil.
Of all the adjustments tried, the graph of log(T + 09) best fits a straight line. Assuming the cooling curve follows an exponential decay function, the final temperature of olive oil in the freezer is −9 °C. I consider this a more reliable answer than −11.2 °C.
practice problem 4
solution
Answer it.